To first order approximation, the results of single molecule measurements of time-dependent processes in a biological system are usually exponentially distributed. This is because we are often measuring the time to an event that has some fixed, independent probability of occurring in any instant (where an instant means a short interval of time).
Think, for example, of radioactive decay: in each instant, an atom in the sample has some fixed probability of decaying (given that it hasn’t already decayed). More precisely, in any given short time interval of length $\Delta t$, we’ll say the probability of a decay occurring in that interval given that it hasn’t already happened is $k \Delta t$, for some proportionality constant $k > 0.$ The average time to decay is then $\tfrac{1}{k}$, and the wait times are exponentially distributed with rate constant $k$.
Keep in mind that this is different from asking how much of the population has decayed at a given point in time: here we are interested in the distribution of individual times to decay, not the amount of un-decayed sample as a function of time. The latter is analogous to ensemble fluorescence measurements (e.g. obtained by measuring signal from a fluorescent dye in a fluorimeter over time).
Very often in biology the process we are observing consists of multiple underlying microscopic events which we cannot observe directly. Each of these events could be governed by an independent exponential process. For example, an enzyme acting on its substrate would first bind the substrate, a process described by one rate constant $k_1$ (i.e., at each time instant, the enzyme would have some probability of binding the substrate, and $k_1$ would have dimension of $\text{time}^{-1}$). Then perhaps a conformational change needs to occur, a process that also has some (different) probability per second of occurring, say $k_2$. And then substrate would be converted to product, with yet another probability per second of occurring, $k_3$. If we measured the times at which product was formed for each substrate molecule in the sample, we would find the distribution of times from substrate to product not to be exponentially distributed. We would instead need some kind of combination of exponentials to describe the overall process.
Most often our experiments only have the resolution to differentiate between one or two exponential processes (or perhaps most strictly, one or more). That is, it’s easiest to determine whether the data are not well described by a single exponential; but whether they are best described by some combination of two exponentials, or three, or more, is usually not possible, in the absence of other information about the system.
Therefore this tutorial will focus on distinguishing between a single exponential distribution, and two kinds of “double” exponentials. “Double exponential” or “bi-exponential” is an under-specified, non-technical term frequently encountered in the single-molecule literature; it usually refers to a hyperexponential distribution, or mixture, with two terms. The other useful “double exponential” is the hypoexponential distribution, which models a sequential process like the enzyme reaction described above. Although the hyperexponential is frequently used, in many cases the hypoexponential is probably a more appropriate model for what we think is happening in the system.
The code in this tutorial can be found in this gist.
Math, part 1: Ways to combine exponential distributions
A hypoexponential describes the total duration of a sequential process: first one thing has to occur, and then a second thing has to occur. If each thing has an independent exponentially distributed duration, then the total duration is the sum of two independent exponential random variables. This is the more common type of process I’ve encountered.
The CDF (see also Histograms vs CDFs) of a two-term hypoexponential has the form $$ \textrm{CDFhypo}(w) = 1-\frac{k_2}{k_2-k_1}e^{-k_1w}+\frac{k_1}{k_2-k_1}e^{-k_2w}, $$ where $w$ is the wait time, and $k_1$ and $k_2$ are the rate constants that describe the two sequential events. $k_1$ and $k_2$ have dimension $\text{time}^{-1}$. This expression gives the probability of having a wait time of $w$ or fewer seconds (or equivalent units). The probability density function (PDF) of this distribution is $$ \textrm{PDFhypo}(w) = \frac{k_1 k_2}{k_1-k_2} \left(e^{-k_2 w}-e^{-k_1 w} \right). $$
For a hypoexponential, the two rate constants that best describe the data can be estimated from data by $$ k_1 = \frac{2}{\mu}\left(1+\sqrt{1+2\left(\frac{\nu^2}{\mu^2}-1\right)}\right)^{-1} $$ $$ k_2 = \frac{2}{\mu}\left(1-\sqrt{1+2\left(\frac{\nu^2}{\mu^2}-1\right)}\right)^{-1} $$ where $\mu$ is the empirical mean of the data and $\nu$ is the standard deviation.
In contrast, the hyperexponential describes a process with a branching pathway: either one thing must occur, or a different thing. The hyperexponential is a mixture of exponentials, and its density is a weighted sum of exponential densities. My favorite example of this kind of process is a mixed population in your sample. Say, for example, you purified a multi-subunit enzyme, but part of your sample lost subunits in the purification process. Perhaps these lost subunits change the enzyme’s rate; then your sample of enzyme would consist of a faster population and a slower population, and your measurement of the wait time to product formation would be best described by a hyperexponential.
(Actually, your measurements of time to product formation would probably really best be described by a branching pathway, with each branch having multiple sequential events as in the hypoexponential above. But we rarely have enough data to get all this information out of our measurements. Instead, if your mixed sample had fairly equal amounts of the two kinds of enzyme, or if those missing subunits really made a big difference in rates, I imagine your data would look more like a hyperexponential–the rates of the two populations would dominate over the rates of each population’s sequential processes. Conversely, if the majority of your sample was one population, or their rates weren’t that different, your data might look more like a hypoexponential.)
The CDF of a two-term hyperexponential is given by $$ \textrm{CDFhyper}(w) = a\left(1-e^{-k_1 w}\right)+(1-a)\left(1-e^{-k_2 w}\right), $$ and the PDF by $$ \textrm{PDFhyper}(w) = a k_1 e^{-k_1 w}+(1-a)k_2e^{-k_2w}, $$ where $a$ is a weighting factor that might correspond to the fraction of the first subpopulation present in the sample. Estimates of the rate constants for a hyperexponential do not have closed-form solutions, but they can be estimated by a maximum likelihood approach as in this gist.
Math, part 2: Distinguishing between combinations of exponentials
There are several approaches to determining whether your data are best described as singly exponentially distributed, hypoexponentially distributed, or hyperexponentially distributed.
One easy way is to calculate the coefficient of variation, which is the standard deviation of the data divided by the mean. If the coefficient of variation is close to one, the data are consistent with a single exponential; if the coefficient of variation is significantly greater than one, the data are consistent with a hyperexponential (branching pathway); if less than one, a hypoexponential (sequential processes). As described below, it is usually best to bootstrap your data and re-compute the coefficient of variation for each bootstrapped sample, and then see whether these bootstrapped coefficients of variation mostly fall around 1, or mostly above 1, or mostly below 1.
Another way of determining exponentiality is by comparing the CDF of your data to the CDFs of a single exponential distribution, a hyperexponential distribution, and a hypoexponential distribution, as in a P-P plot (code and example plots given below).
Code
Generate data
We will generate three synthetic data sets, one drawn from a single exponential distribution, one from a hypoexponential, and one from a hyperexponential. The single exponential will have a rate constant of $k_1$ = 1⁄5 per second (mean wait time of 5 seconds), and the two-term exponentials will have rate constants $\mathit{kh}_1$ = 1⁄5 per second and $\mathit{kh}_2$ = 1⁄50 per second. The hyperexponential will have a weighting factor of 0.3 (one population is 30% of the total). Each data set will have 100 samples:
k1 = 1/5;
kh = [1/50, 1/5];
a = 0.3;
n_samples = 100;
data_single = exprnd(1/k1, 1, n_samples); % Requires the statistics toolbox
data_hypo = exprnd(1/kh(1), 1, n_samples) + exprnd(1/kh(2), 1, n_samples);
data_hyper = exprnd(1./kh(double(rand(1, n_samples) > a) + 1));
Test for different kinds of exponentiality
First let’s calculate the coefficient of variation of each data set, as well as a bootstrapped estimate of our uncertainty about that coefficient of variation:
cv_single = std(data_single) / mean(data_single);
cv_hypo = std(data_hypo) / mean(data_hypo);
cv_hyper = std(data_hyper) / mean(data_hyper);
num_bs = 500;
cv_single_bs = bootstrp(num_bs, @(x) std(x) / mean(x), data_single);
cv_hypo_bs = bootstrp(num_bs, @(x) std(x) / mean(x), data_hypo);
cv_hyper_bs = bootstrp(num_bs, @(x) std(x) / mean(x), data_hyper);
(See also https://stephlj.github.io/tutorials/Bootstrapping for more information on bootstrapping.)
I’m not usually a fan of histograms (see https://stephlj.github.io/tutorials/HistosVsCDFs), but for a quick-and-dirty, non-quantitative look at the data, they’re ok:
function PlotHisto(fig_handle, cv_bs, cv_mean, fig_title)
[n, xout] = hist(cv_bs);
n = n ./ length(cv_bs);
subplot(fig_handle)
bar(xout, n)
xlabel('Coefficient of variation', 'Fontsize', 16)
ylabel('Frequency', 'Fontsize', 16)
title(fig_title, 'Fontsize', 16)
set(gca, 'Fontsize', 16)
hold on
plot([cv_mean cv_mean], [0 max(n)], '--r')
plot([1 1], [0 max(n)], '--k')
hold off
end
figure
h1=subplot(1,3,1)
PlotHisto(h1, cv_single_bs, cv_single, 'Single exp')
h2=subplot(1,3,2)
PlotHisto(h2, cv_hypo_bs, cv_hypo, 'Hypo exp')
h3=subplot(1,3,3)
PlotHisto(h3, cv_hyper_bs, cv_hyper, 'Hyper exp')
Figure 1 shows the resulting histograms of bootstrapped coefficients of variation. As expected,
the single exponential data have a coefficient of variation clustered around 1, the hypoexponential clusters
significantly below 1, and the hyperexponential clusters above 1.

Histograms of bootstrapped coefficients of variation for an exponential distribution, and combinations of exponentials.
Another way to assess which distribution best describes your data is to use a P-P plot, which compares the empirical CDF of your data to the theoretical CDF of a fit distribution you’re testing against. Code for a P-P plot in Matlab can be found in this gist.
How do our three data sets compare to the three distributions? See the gist for the code that generated Figure 2:
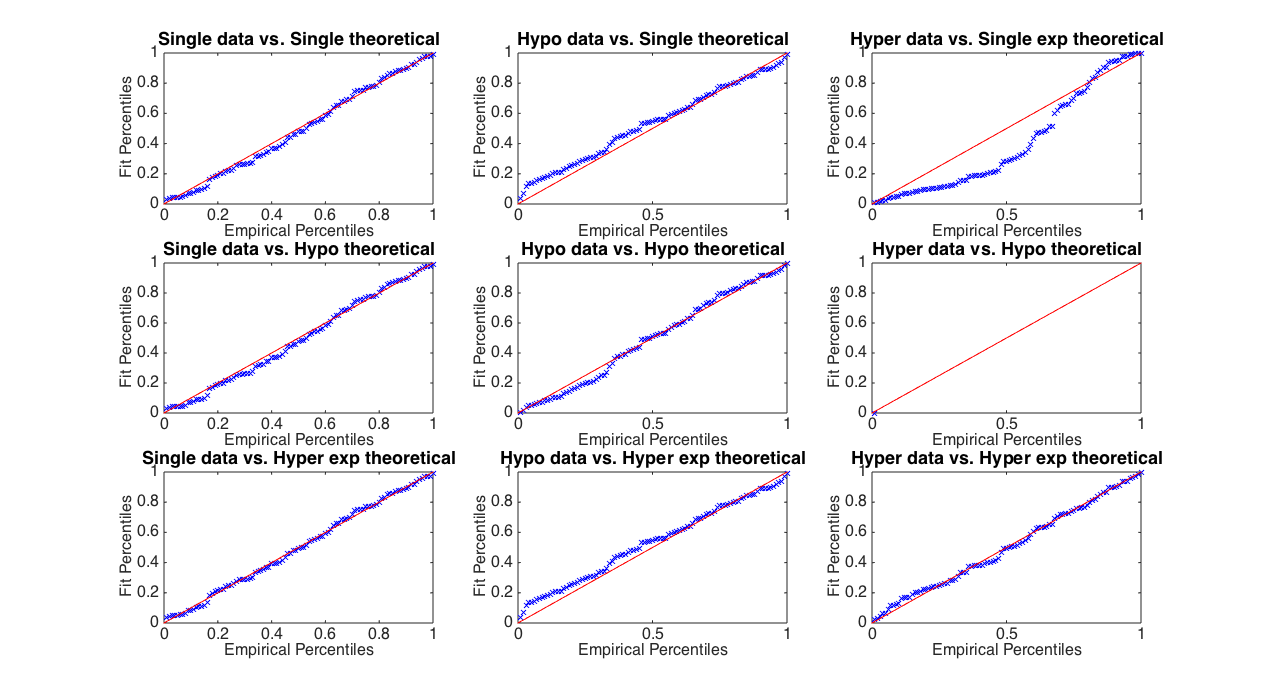
P-P plots comparing synthetic data to different types of exponential distributions.
These P-P plots give us more information than the coefficients of variation: if the data are well-described by whatever distribution we’re testing against, as on the diagonal from top left to bottom right, then the results of the P-P plot should fall along the $y=x$ line. If they don’t, that tells you something about how your data differ from the theoretical distribution you’re comparing to. For example, if the empirical data are smaller than the theoretical data at high percentiles, such that the P-P results fall above the $y=x$ line, as in the top right panel, your data have a heavier tail than the distribution you’re comparing to.
Looking at Figure 2, we can see first of all that single exponentially distributed data are well-fit by all three theoretical distributions. That makes sense; if we add more parameters and more terms, we simply over-fit the data. Hyperexponentially distributed data are particularly poorly fit by a single exponential, as indicated by the large deviation from the $y=x$ line. Note that we are unable to generate a theoretical hypoexponential distribution for the hyperexponential data, because their coefficient of variation is greater than 1, and that means we end up with a negative rate constant for $k_2$—remember that these rate constants must be greater than zero!
Concluding remarks: other distributions encountered in biology
Various kinds of exponential distributions are common in biology and especially in single-molecule measurements. If you’re measuring something to do with rates, or time, you’ll likely be measuring something that is either exponentially distributed or comprises exponentially distributed components.
We note briefly some contexts in which other kinds of distributions may arise. In all of these cases, similar approaches (e.g. P-P plots) to those described above for exponentials can be used to test whether your data are consistent with some theoretical distribution.
Geometric distributions
The geometric distribution is the discretized analog to the exponential distribution. We usually assume that the underlying natural process we are measuring is governed by the exponential distribution, but often our measurements of said process occur in discretized increments (for example, discretized by the frame rate of a microscope camera). Whether you use a geometric distribution or an exponential distribution will depend on how much this discretization process matters.
Gaussian
Gaussian distributions are another common distribution in biology and in single-molecule biophysics—for example, the intensity of a stable fluorescent molecule over time will be Gaussian-distributed around some mean value. We usually assume noise is Gaussian.
Note that a common point of confusion about Gaussian-distributed samples versus exponential samples is what the mean value of the samples represents. For a Gaussian-distributed set of measurements (in one dimension), the most frequently observed values will cluster around the mean of the Gaussian. For exponentially distributed samples, however, most samples will have values less than the mean.
Poisson/Binomial
A classic example of a binomial process in biology is dilution of a cytoplasmic factor over the course of several generations of cell division. The distribution of how many of these factors each daughter cell will have over time will be binomial. Alternatively, consider how many mRNAs are produced per unit time. Notice that here we’re not interested in measuring the wait time to something, even though it sounds like there’s a time component here. We’re really measuring how many of something in a unit of time.
Thanks to Matt Johnson for teaching me this material, and for editing this tutorial for accuracy and clarity!